Reference : harmonic series
When we hear a sound produced by a musical instrument, we are actually hearing a multiplicity of sounds that form the harmonic series. In the 17th century, the Frenchman Joseph Sauveur (1653-1716) and the Englishman Thomas Pigot (1657-1686) noticed that the strings vibrate in sections, a phenomenon that explains why one string produces this multiplicity of sounds.
The video below shows the spectral analysis of a C two octaves below the middle C (C2):
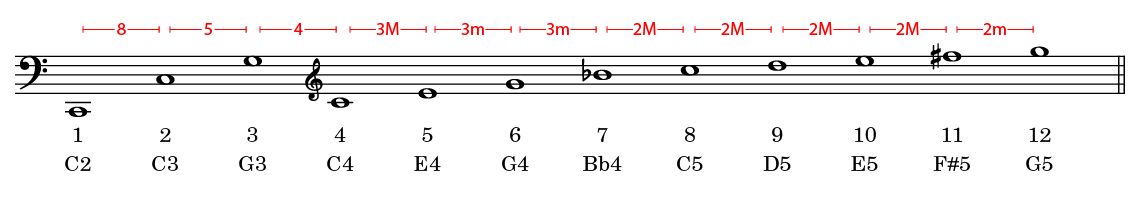
Notes:
- We have written the musical notes corresponding to the first 12 harmonics of the series. It is obvious that many harmonics follow these first harmonics.
- The first harmonic or fundamental is not necessarily the strongest harmonic.
- The balance between harmonics is constantly changing. This, together with the immense number of harmonics, explains the difficulty we encounter in synthesizing sounds.
Importance of the Harmonic Series
The harmonic series defines many of our intervals. Listed below are the octave, fifth, fourth, major third and minor seventh:
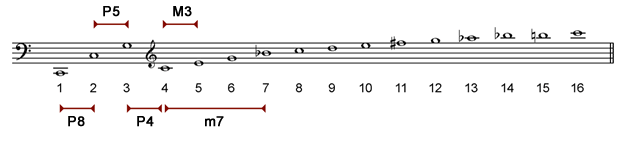
We can calculate mathematical ratio (or size) by dividing the frequencies of notes. Here we use the frequency of some harmonics to calculate the size of intervals:
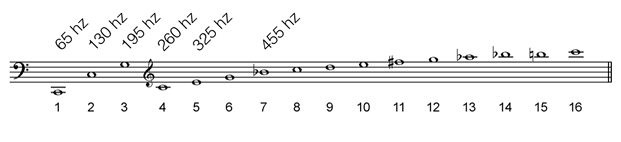
| Interval | Ratio | From the harmonics |
|---|---|---|
| Octave | 130 / 65 = 2 | 1 and 2 |
| Fifth | 195 / 130 = 1.5 | 2 and 3 |
| Fourth | 260 / 195 = 1.33 | 3 and 4 |
| Major third | 325 / 260 = 1.25 | 4 and 5 |
| Minor seventh | 455 / 260 = 1.75 | 4 and 7 |
Interestingly we can calculate the values using harmonic numbers:
| Interval | Ratio | From the harmonics |
|---|---|---|
| Octave | 2 / 1 = 2 | 1 and 2 |
| Fifth | 3 / 2 = 1.5 | 2 and 3 |
| Fourth | 4 / 3 = 1.33 | 3 and 4 |
| Major third | 5 / 4 = 1.25 | 4 and 5 |
| Minor seventh | 7 / 4 = 1.75 | 4 and 7 |
Calculating frequencies
The mathematical ratios can be used to calculate the frequency of notes. From an A 440 we calculate the frequency of C#, E and G:
| A | C# (major third) | E (perfect fifth) | G (minor seventh) |
| 440 | 440 x 1.25 = 550 | 440 x 1.5 = 660 | 440 x 1.75 = 770 |
If we divide by the mathematical ratio we obtain descending intervals. Here we calculate the frequency of an F, a major third below A:

